Часть 7-1 Местные сопротивления, приборы для измерения расхода и скорости

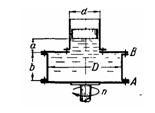
Задача (Куколевский И.И.) 4-18. Изображенный на чертеже сосуд имеет размеры D = 0,4 м; d = 0,2 м, b = 0,35 м и наполнен водой до высоты а+b = 0,52 м. Сверху сосуд закрыт поршнем, имеющим вес G = 50 кГ. Определить гидравлические нагрузки болтовых групп А и В, если сосуд вращается относительно центральной вертикальной оси с числом оборотов n = 450 об/мин. Трением между поршнем и стенками цилиндра пренебречь. Указание. При вращении системы суммарная сила давления жидкости на поршень равна весу поршня. Это условие позволяет найти давление в центре поршня и, следовательно, во всех точках сосуда.
Ответ. РА=РВ = 3710 Н.

Скачать решение задачи 4-18 (Куколевский И.И.)

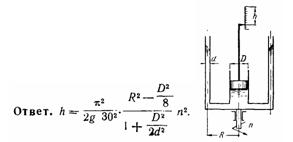
Задача (Куколевский И.И.) 4-19. Жидкостный тахометр состоит из цилиндра, наполненного ртутью и сообщенного с двумя трубками малого диаметра d, расположенными на расстоянии R от оси. Цилиндр снабжен поршнем, имеющим диаметр D и вес G. Поршень перемещается при изменении числа оборотов тахометра. Установить связь между числом оборотов n тахометра и опусканием h поршня от его начального положения при невращающемся тахометре.

Скачать решение задачи 4-19 (Куколевский И.И.)

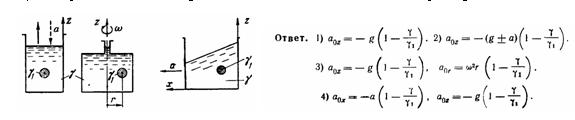
Задача (Куколевский И.И.) 4-20. В жидкости удельного веса у удерживается в равновесии тело удельного веса у1. Определить, какое начальное ускорение a0, по отношению к жидкости приобретет тело, если его освободить, при условии., что: 1)сосуд, содержащий жидкость, неподвижен; 2) сосуд движется вертикально (вверх или вниз) с постоянным ускорением а; 3) сосуд равномерно вращается относительно вертикальной оси с угловой скоростью w; 4) сосуд движется горизонтально с постоянным ускорением а.

Скачать решение задачи 4-20 (Куколевский И.И.)

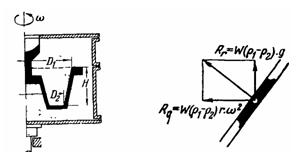
Задача (Куколевский И.И.) 4-21. Определить минимальное число оборотов литейной формы, при котором легкие включения имеют возможность выделиться из расплавленного металла в середину формы, при следующих размерах отливаемой детали: D1 = 300 мм; D2 = 200 мм; Н = 300 мм. Указание. Условия относительного движения легкой частицы во вращающейся литейной форме определяются действием на нее сил давления жидкого металла Р, собственного веса частицы G и переносной силы инерции J. Направление результирующей К этих сил обеспечивает при любом числе оборотов перемещение легких включений по внутреннему наклонному и горизонтальному каналам формы к ее центру. По внешнему наклонному каналу (см. рис. к задаче 4-21) легкие включения могут перемещаться к центру формы лишь в том случае, когда результирующая R имеет составляющую, направленную вдоль стенки вниз.
Ответ, n = 231 об/мин.

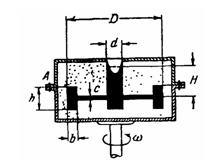
Задача (Куколевский И.И.) 4.22 Отливка чугунного колеса диаметром D = 1 000 мм, с ободом высотой h = 200 мм и толщиной b = 80 мм, диском толщиной с = 40 мм и ступицей диаметром d = 200 мм производится во вращающуюся с n = 200 об/мин земляную форму. Определить растягивающую силу в болтовой группе А опоки, не учитывая веса опоки и земли. Высота заполнения формы Н = 300 мм, удельный вес жидкого чугуна у = 7 200 кГ/м3. Ответ. РА = 167 Н.

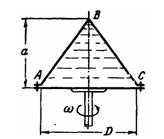
Задача (Куколевский И.И.) 4-23. Определить силу давления на коническую боковую поверхность АВС и плоское дно АС сосуда, целиком заполненного водой и вращающегося с угловой скоростью wо = 20 рад/с, если известно, что в верхней точке В сосуда вакуум равен рв = 20 кПа. Размеры сосуда: D=1 м; а = 1 м.
Ответ. РАВС = 9,38 кН; РАС = I 2 кН.

Скачать решение задачи 4-23 (Куколевский И.И.)

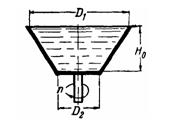
Задача (Куколевский И.И.) 4-24. Определить наименьшее число оборотов, при котором полностью опорожнится предварительно заполненный жидкостью Открытый конический сосуд, имеющий диаметры D1 = 460 мм; D2=200 мм и высоту H0 = 75 мм. Указание. Полное опорожнение сосуда произойдет при таком числе оборотов, когда свободная поверхность жидкости коснется стенки сосуда у его дна и вектор суммарной массовой силы, действующей на последнюю частицу жидкости в этой точке, окажется нормальным к стенке.
Ответ. n = 71,7 об /мин.

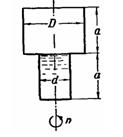
Задача (Куколевский И.И.) 4-25. Сосуд, вращающийся относительно вертикальной оси, состоит из двух цилиндров одинаковой высоты а = 200 мм и диаметров d=150 мм. и D = 300 мм. Нижний цилиндр целиком заполнен жидкостью. При каком числе оборотов жидкость начнет выливаться из сосуда? Отметить качественное влияние размеров а, d и D сосуда на искомое число оборотов. Ответ, n = 252 об /мин.

Скачать решение задачи 4-25 (Куколевский И.И.)

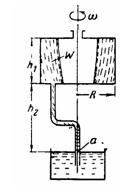
Задача (Куколевский И.И.) 4-26. Цилиндрический сосуд радиуса R = 250 мм и высоты h1 = 300 мм, заполненный объемом жидкости W = 45 дм3, вращается относительно центральной вертикальной оси. Ко дну сосуда присоединена изогнутая трубка, ось нижнего конца которой совпадает с осью вращения сосуда. Конец трубки опущен под уровень неподвижной жидкости, расположенный ниже дна верхнего сосуда на h2 = 460 мм. 1) Определить угловую скорость w* вращения сосуда, при которой жидкость во вращающейся трубке находится в относительном покое. 2) Выяснить направление движения жидкости в трубке при w>< w*. Указание. Относительный покой жидкости в трубке возможен только при условии, что давление в точке а трубки на уровне свободной поверхности в неподвижном сосуде равно атмосферному и что, следовательно, вершина параболоида пьезометрической поверхности проходит через эту точку
Ответ, w*=30 рад/с

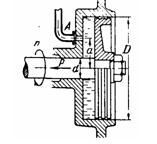
Задача (Куколевский И.И.) 4-27. Гидравлическая пята, вращающаяся с числом оборотов n = 3000 об/мин, получает воду по трубке А под давлением р= 10 атм. Определить осевую силу Р, которую может уравновешивать пята, считая, что вода под поршнем вращается с половиной угловой скорости вращения последнего. Диаметр поршня D = 0,32 м, диаметр вала d = 0,05 м, трубка присоединена к корпусу пяты на расстоянии а = 0,07 м от оси. На каком расстоянии от оси нужно расположить трубку А, чтобы осевая сила, уравновешиваемая пятой, не зависела от оборотов?
Ответ. Р = 86 кН, а =0,113 м.

Скачать решение задачи 4-27 (Куколевский И.И.)

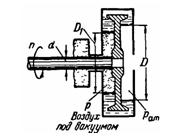
Задача (Куколевский И.И.) 4-28. Определить диаметр D1 на котором установится вода во внутренней полости гидравлического уплотнения вала воздушной машины, если диаметр вала d = 0,15 м, диаметр, на котором установилась вода в наружной полости уплотнения, О = 0,3 м и вакуум во внутренней полости Pв = 0,7 ат. Вал вращается с числом оборотов n = 2000 об/мин, а угловая скорость вращения воды равна половине угловой скорости вращения вала. Определить осевое усилие, передаваемое на вал диском уплотнения.
Ответ. D1 = 20 см; Р = 2,3 кН.

Скачать решение задачи 4-28 (Куколевский И.И.)

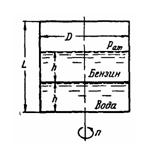
Задача (Куколевский И.И.) 4-29. Замкнутый цилиндрический сосуд размерами D = 400 мм и L = 400 мм, вращающийся с числом оборотов n = 3000 об/мин, заполнен равными объемами воды и бензина (б = 0,7), образующими слои одинаковой высоты h = 150 мм. Определить, пренебрегая весомостью жидкости: 1) Наибольшее давление в сосуде. 2) Растягивающие усилия Р1 и P2 в осевом сечении сосуда и в сечении, перпендикулярном его оси.
Ответ. 1) ри = 1,25 МПа. 2) P1 = 202 кН; P2= 54 кН.

 

Скачать решение задачи 4-29 (Куколевский И.И.)

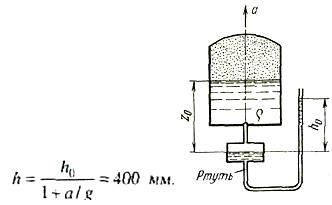
Задача (Куколевский И.И.) 4.30. Показание ртутного чашечного манометра, присоединенного к замкнутому баку, в котором находится жидкость плотностью р = 1500 кг/м3, равно h0 = 800 мм. Как изменится показание манометра, если системе сообщить поступательное ускорение, направленное вверх и равное ускорению свободного падения (a=g)? Изменениями уровня жидкости в баке и ртути в чашке манометра пренебречь (z0= 1 м); давление газа в баке считать неизменным. Рассмотреть, частный случай, когда ноль шкалы манометра находится на уровне жидкости в баке (z0 = 0).
Ответ. h = 455 мм; при z0= 0 показание манометра

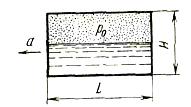
Задача (Куколевский И.И.) 4.31. Закрытый призматический сосуд размерами L*H*C = 3*1*1 м до середины высоты заполнен водой, над уровнем которой имеется избыточное давление газа Po = 50 кПа. Сосуд движется горизонтально с постоянным ускорением а = 0.5*g. Определить силы давления на заднюю стенку (Рз) и дно (Рд) сосуда. Как повлияет на силы давления отсутствие поля сил тяжести?
Ответ. Рз = 57,36 кН и Рд=165.3кН; Рз =57,36кН и Рд=155,5кН.

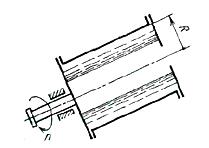
Задача (Куколевский И.И.) 4.32. Цилиндрический сосуд радиусом R= 100 мм, заполненный водой на 3/4 своего объема, вращается равномерно с частотой n= 10 000 об/мин относительно своей оси. Пренебрегая действием силы тяжести, определить силу давления воды на торцовую стенку сосуда.
Ответ. P = 48,2 кН.

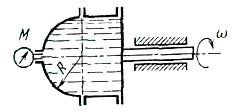
Задача (Куколевский И.И.) 4.33. Определить силу давления воды па полусферическую крышку цилиндрического сосуда радиусом R = 0,2 м, если сосуд вращается относительно своей оси с угловой скоростью w= 100 рад/с и манометр при этом показывает давление М = 50кПа. Действием силы тяжести на жидкость пренебречь.
Ответ. Р=18,8 кН.

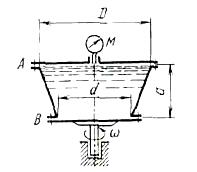
Задача (Куколевский И.И.) 4.34. Конический сосуд размерами d = 0,6 м. D= 1 м, а = 0,9 м заполнен водой и приведен в равномерное вращение с угловой скоростью w = 20 рад/с. Давление в центре крышки сосуда по манометру М = 10 кПа. Определить гидравлические нагрузки болтовых групп А и В сосуда: 1) учитывая действие силы тяжести; 2) пренебрегая действием этой силы.
Ответ. РA = 27,7 кН; 1) PB= 3.34 кН; 2) PB= 5,37 кН.

Скачать решение задачи 4-34 (Куколевский И.И.)

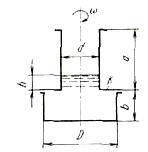
Задача (Куколевский И.И.) 4.35. Цилиндрический сосуд с горловиной, размеры которого d = 0,2 м, D = 0,4 м, а = 0,4 м и b = 0,2 м, равномерно вращается вокруг своей вертикальной оси. Сосуд предварительно заполнен жидкостью (р = 1325 кг/м3) до высоты h = 0,1 м в горловине. Найти угловую скорость со сосуда, при которой из него начнет выливаться жидкость. При этой угловой скорости определить силу давления Р жидкости на крышку К сосуда. Как изменятся сила давления на крышку, если угловая скорость станет вдвое больше найденной?
Ответ, w= 34,3 рад/с; Р= 1600 и 4900 Н.

Скачать решение задачи 4-35 (Куколевский И.И.)

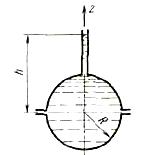
Задача (Куколевский И.И.) 4.36. Определить силу давления на верхнюю половину шара радиусом R=0,6 м, заполненного водой до уровня h= 1,2 м в пьезометре, в следующих четырех случаях: 1} шар неподвижен; 2) вращается вокруг вертикальной оси с угловой скоростью w = 12 рад/с, 3) свободно падает и поле силы тяжести; 4} свободно падает вращаясь с угловой скорости w=12 рад/с.
Ответ Р = 8,8; 23,5; 0 и 14,7 кН.

Скачать решение задачи 4-36 (Куколевский И.И.)